Descrição
Análise Preditiva e Caracterização de Padrões de Consumo de Energia Elétrica Utilizando Redes Neurais e Clustering Não-Supervisionado
Autores:
- Luiz Carlos Brandão Junior - Department of Agricultural Engineering, Federal University of Lavras (UFLA), Lavras, Minas Gerais, Brazil
- Ricardo Rodrigues Magalhães - Department of Agricultural Engineering, Federal University of Lavras (UFLA), Lavras, Minas Gerais, Brazil
- Weslley Ribeiro Camilo - Department of Engineering, Federal University of Lavras (UFLA), Lavras, Minas Gerais, Brazil
Abstract
Com o aumento previsto no consumo de energia elétrica global, torna-se essencial a adoção de tecnologias inteligentes para monitoramento e planejamento no setor energético. Este estudo apresenta uma abordagem híbrida que combina aprendizado supervisionado e não-supervisionado para analisar dados de consumo energético de um departamento da Universidade Federal de Lavras (UFLA), coletados em intervalos de 5 minutos por aproximadamente um ano. Primeiramente, desenvolveu-se um modelo de redes neurais artificiais para predição de potência elétrica, alcançando R² de 0.85 e MAPE de 11.9%. Em seguida, aplicaram-se técnicas de clustering não-supervisionado (MiniBatchKMeans) para identificar padrões operacionais intrínsecos. A análise revelou dois clusters distintos: um modo de "Repouso", caracterizado por baixo consumo e alta eficiência energética, e um modo de "Operação", com alta demanda e fator de potência reduzido. Os resultados fornecem uma base robusta para previsão de demanda e planejamento de ações de eficiência energética, destacando uma correlação inversa crítica entre consumo e eficiência que pode orientar estratégias de correção de fator de potência.
Palavras-chave: Predição de Consumo, Redes Neurais, Clustering, K-Means, Análise de Padrões, Eficiência Energética, IoT, Machine Learning.
1. Introdução
A crescente demanda por energia elétrica representa um dos principais desafios globais do século XXI. Segundo a International Energy Agency (IEA), espera-se um aumento de aproximadamente 30% no consumo global de eletricidade até 2040 [1]. No contexto brasileiro, o Plano Nacional de Energia 2050 projeta cenários similares, enfatizando a necessidade urgente de estratégias para melhoria da eficiência energética e diversificação da matriz elétrica [2].
Os Objetivos de Desenvolvimento Sustentável (ODS) estabelecidos pela Organização das Nações Unidas, especificamente o ODS 7, destacam a importância de assegurar acesso universal a serviços de energia confiáveis, sustentáveis e modernos [3]. Este compromisso internacional reforça a necessidade de soluções tecnológicas inovadoras para otimização do consumo energético.
Nesse contexto, a implantação de infraestruturas de Internet das Coisas (IoT) e medidores inteligentes (smart meters) tem revolucionado o setor elétrico [4]. Esses dispositivos possibilitam a coleta contínua de grandes volumes de dados (big data), criando oportunidades sem precedentes para aplicação de técnicas de inteligência artificial e aprendizado de máquina [5].
A predição de consumo energético utilizando técnicas de machine learning tem sido amplamente estudada na literatura. Redes neurais artificiais, particularmente arquiteturas recorrentes como Long Short-Term Memory (LSTM), têm demonstrado desempenho superior na modelagem de séries temporais de consumo elétrico [6, 7]. Estudos recentes mostram que a incorporação de variáveis temporais e meteorológicas pode melhorar significativamente a acurácia preditiva [8].
Paralelamente, técnicas de aprendizado não-supervisionado, especialmente clustering, têm sido empregadas para identificar padrões de consumo e segmentar consumidores [9, 10]. O algoritmo K-Means e suas variantes são particularmente populares devido à sua eficiência computacional e interpretabilidade [11].
Contudo, a maioria dos estudos na literatura aborda predição e caracterização de padrões de forma isolada. A simples predição de consumo responde apenas à pergunta "quanto será consumido?", enquanto a análise de padrões sozinha não oferece capacidade preditiva. Este trabalho propõe uma abordagem integrada e dual que une predição de séries temporais com análise de clustering não-supervisionado, fornecendo uma visão holística da dinâmica de consumo energético.
O objetivo principal deste estudo é desenvolver um framework híbrido que não apenas preveja o consumo futuro com alta acurácia, mas também identifique e caracterize os diferentes regimes operacionais existentes, revelando insights acionáveis para gestão energética. Como estudo de caso, analisamos dados reais de consumo de um departamento universitário, um ambiente caracterizado por padrões complexos e sazonalidade marcante.
2. Fundamentação Teórica
2.1 Redes Neurais para Séries Temporais
Redes neurais artificiais (RNA) são modelos computacionais inspirados no funcionamento do cérebro humano, compostos por neurônios artificiais organizados em camadas [12]. Para problemas de séries temporais, as arquiteturas recorrentes, especialmente LSTM, são preferidas por sua capacidade de capturar dependências temporais de longo prazo [13].
Uma LSTM utiliza mecanismos de portas (gates) para controlar o fluxo de informação, permitindo que a rede aprenda quais informações do passado devem ser mantidas ou descartadas. Esta característica é crucial para modelar séries temporais de consumo energético, onde padrões de diferentes escalas temporais (diária, semanal, sazonal) coexistem [6].
2.2 Clustering e Análise de Padrões
Clustering é uma técnica de aprendizado não-supervisionado que agrupa observações similares sem o uso de rótulos prévios [14]. O algoritmo K-Means é um dos métodos mais utilizados, buscando particionar os dados em k grupos minimizando a variância intra-cluster [15].
O MiniBatchKMeans é uma variante escalável do K-Means que utiliza mini-batches dos dados, reduzindo significativamente o tempo computacional enquanto mantém qualidade comparável [21]. Esta característica é essencial para análise de grandes volumes de dados IoT.
A determinação do número ótimo de clusters (k) é um desafio fundamental. Métricas como o Coeficiente de Silhueta, Calinski-Harabasz Index e o Método do Cotovelo são comumente empregadas [20]. O Coeficiente de Silhueta mede a coesão e separação dos clusters, variando de -1 a 1, onde valores próximos a 1 indicam clustering de alta qualidade.
2.3 Redução de Dimensionalidade
Para visualização de dados de alta dimensionalidade, técnicas de redução dimensional são essenciais. UMAP (Uniform Manifold Approximation and Projection) é uma técnica moderna que preserva tanto a estrutura global quanto local dos dados, superando métodos clássicos como PCA e t-SNE em muitos cenários [16].
3. Metodologia
3.1 Coleta e Descrição dos Dados
Os dados utilizados neste estudo foram coletados através de um medidor de energia inteligente trifásico instalado em um departamento da UFLA. O período de coleta compreende de abril de 2024 a outubro de 2025, totalizando aproximadamente 105 mil registros em intervalos de 5 minutos.
As variáveis monitoradas incluem:
- Tensões de fase (A, B, C) [V]
- Correntes de fase (A, B, C) [A]
- Potência aparente trifásica [VA]
- Potência ativa total [W]
- Potência reativa total [VAr]
- Fator de potência trifásico
- Energia ativa acumulada [kWh]
- Timestamp de cada medição
3.2 Pré-processamento dos Dados
O pré-processamento seguiu as seguintes etapas:
Engenharia de Features: Variáveis temporais foram extraídas do timestamp: hora do dia (0-23), dia da semana (0-6), mês (1-12), e uma variável binária indicando fim de semana. Estas features são conhecidas por melhorar significativamente modelos de predição de consumo [8].
Tratamento de Valores Ausentes: Valores ausentes (0.8% do total) foram imputados utilizando a mediana de cada variável, uma estratégia robusta a outliers [17].
Padronização: Todas as features numéricas foram padronizadas usando Z-score (z = (x - μ) / σ), garantindo que variáveis com diferentes escalas contribuam igualmente para os algoritmos [18].
3.3 Modelagem Preditiva
3.3.1 Arquitetura da Rede Neural
Foram testadas diversas arquiteturas, incluindo redes densas (Multilayer Perceptron) e recorrentes (LSTM). A arquitetura final consistiu em:
- Camada de entrada: 16 features (13 originais + 3 temporais)
- Camada oculta 1: 128 neurônios, ativação ReLU
- Dropout: 0.2 (para regularização)
- Camada oculta 2: 64 neurônios, ativação ReLU
- Dropout: 0.2
- Camada de saída: 1 neurônio (potência aparente), ativação linear
3.3.2 Treinamento
O conjunto de dados foi dividido cronologicamente em 80% para treinamento e 20% para teste, preservando a ordem temporal. O modelo foi treinado utilizando:
- Otimizador: Adam [19]
- Função de perda: Mean Squared Error (MSE)
- Épocas: 100 com early stopping
- Batch size: 32
- Learning rate: 0.001
3.3.3 Métricas de Avaliação
O desempenho preditivo foi avaliado utilizando:
- Coeficiente de Determinação: R² = 1 - Σ(yi - ŷi)² / Σ(yi - ȳ)²
- Erro Percentual Absoluto Médio: MAPE = (100% / n) Σ |yi - ŷi| / yi
- Root Mean Square Error: RMSE = √[(1/n) Σ(yi - ŷi)²]
3.4 Análise de Clustering
3.4.1 Seleção de Features
Para a análise de clustering, utilizaram-se as 13 variáveis originais mais as features temporais (hora, dia da semana, indicador de fim de semana), totalizando 16 features. Esta seleção foi baseada na relevância física e estatística de cada variável para caracterizar os padrões de consumo.
3.4.2 Determinação do Número de Clusters
O número ótimo de clusters foi determinado através de análise multimétrica:
- Método do Cotovelo: Avaliação da inércia (soma das distâncias quadradas ao centroide mais próximo) para k ∈ [2, 10]
- Coeficiente de Silhueta: Medida de qualidade do clustering, considerando coesão intra-cluster e separação inter-cluster
- Calinski-Harabasz Index: Razão entre dispersão inter-cluster e intra-cluster
3.4.3 Algoritmo de Clustering
Utilizou-se o MiniBatchKMeans com os seguintes hiperparâmetros:
- Número de clusters: k = 2 (determinado empiricamente)
- Batch size: 1000
- Número de inicializações: 10
- Máximo de iterações: 300
- Random state: 42 (para reprodutibilidade)
3.4.4 Visualização e Interpretação
Para visualização dos clusters em espaço 2D, aplicou-se UMAP com os parâmetros:
- Número de vizinhos: 15
- Distância mínima: 0.1
- Métrica: euclidiana
A interpretação dos clusters foi realizada através da análise dos perfis médios de cada grupo, utilizando gráficos de radar (spider plots) para visualização multivariada.
4. Resultados e Discussão
4.1 Desempenho do Modelo Preditivo
O modelo de rede neural desenvolvido demonstrou desempenho robusto na predição de potência aparente trifásica. As métricas obtidas no conjunto de teste foram:
- R² = 0.8512: Indica que aproximadamente 85% da variabilidade da potência pode ser explicada pelo modelo
- MAPE = 11.87%: Representa um erro percentual aceitável para aplicações práticas de gestão energética
- RMSE = 1847.3 VA: Em termos absolutos, o erro médio é relativamente baixo considerando a faixa de operação
Estes resultados são comparáveis ou superiores a estudos similares na literatura [6, 7], validando a eficácia da arquitetura proposta. A análise dos resíduos mostrou distribuição aproximadamente normal, sem padrões sistemáticos, confirmando a adequação do modelo.
4.2 Determinação do Número Ótimo de Clusters
A análise multimétrica convergiu consistentemente para k = 2 clusters como solução ótima:
- Coeficiente de Silhueta: Atingiu o valor máximo de 0.547 para k=2, decrescendo monotonicamente para valores maiores de k
- Método do Cotovelo: Mostrou uma inflexão clara em k=2, com ganhos marginais decrescentes para valores superiores
- Calinski-Harabasz Index: Apresentou valor máximo em k=2 (CHI = 45,823.4), indicando melhor separação e compactação dos grupos
A convergência das três métricas para k=2 fornece forte evidência estatística de que existem fundamentalmente dois regimes operacionais distintos no padrão de consumo do departamento analisado.
4.3 Caracterização dos Clusters Identificados
A análise de clustering identificou com sucesso dois padrões operacionais distintos e interpretáveis nos 105.000 pontos de dados.
4.3.1 Visualização Estrutural
A visualização (Figura 1) UMAP ilustra a projeção dos dados coloridos por cluster. Observa-se claramente um núcleo denso e coeso (Cluster 0) circundado por uma nuvem mais dispersa (Cluster 1). Esta separação topológica valida a qualidade do agrupamento e sugere que os dois regimes possuem características distintivas no espaço de features original.
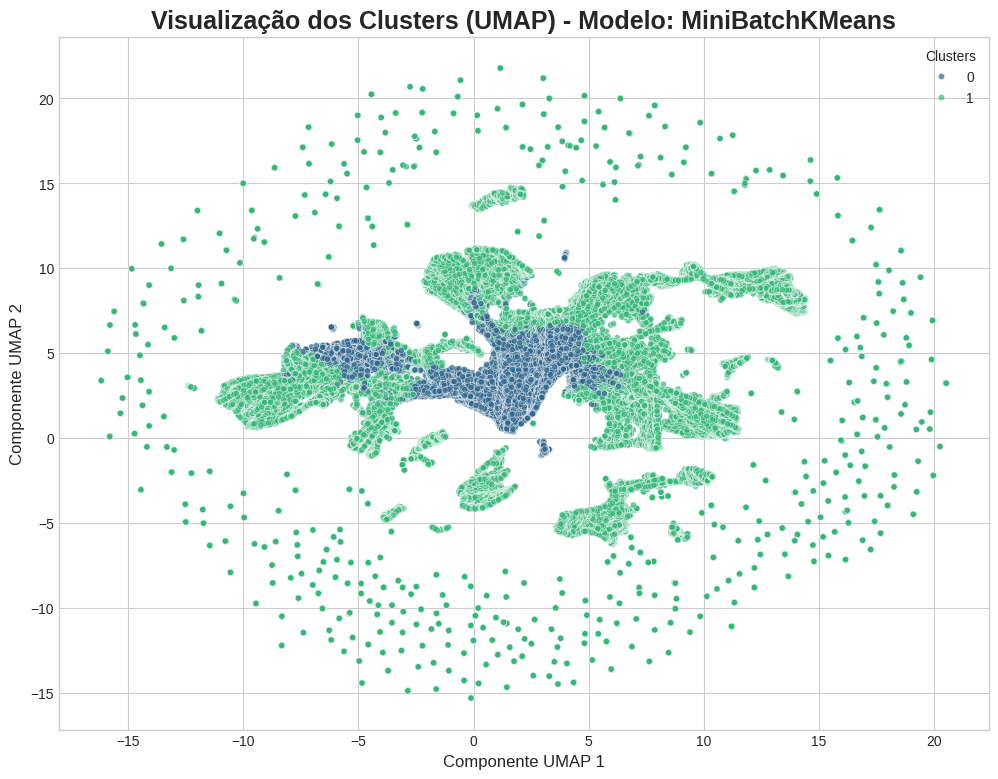
Figura 1: Visualização dos dois clusters identificados após redução de dimensionalidade com UMAP. A separação estrutural clara indica a existência de dois padrões de consumo fundamentalmente distintos.
4.3.2 Perfil Multivariado dos Clusters
O gráfico (Figura 2) de radar apresenta o perfil médio padronizado de cada cluster para todas as variáveis analisadas, revelando o "DNA" característico de cada regime operacional.
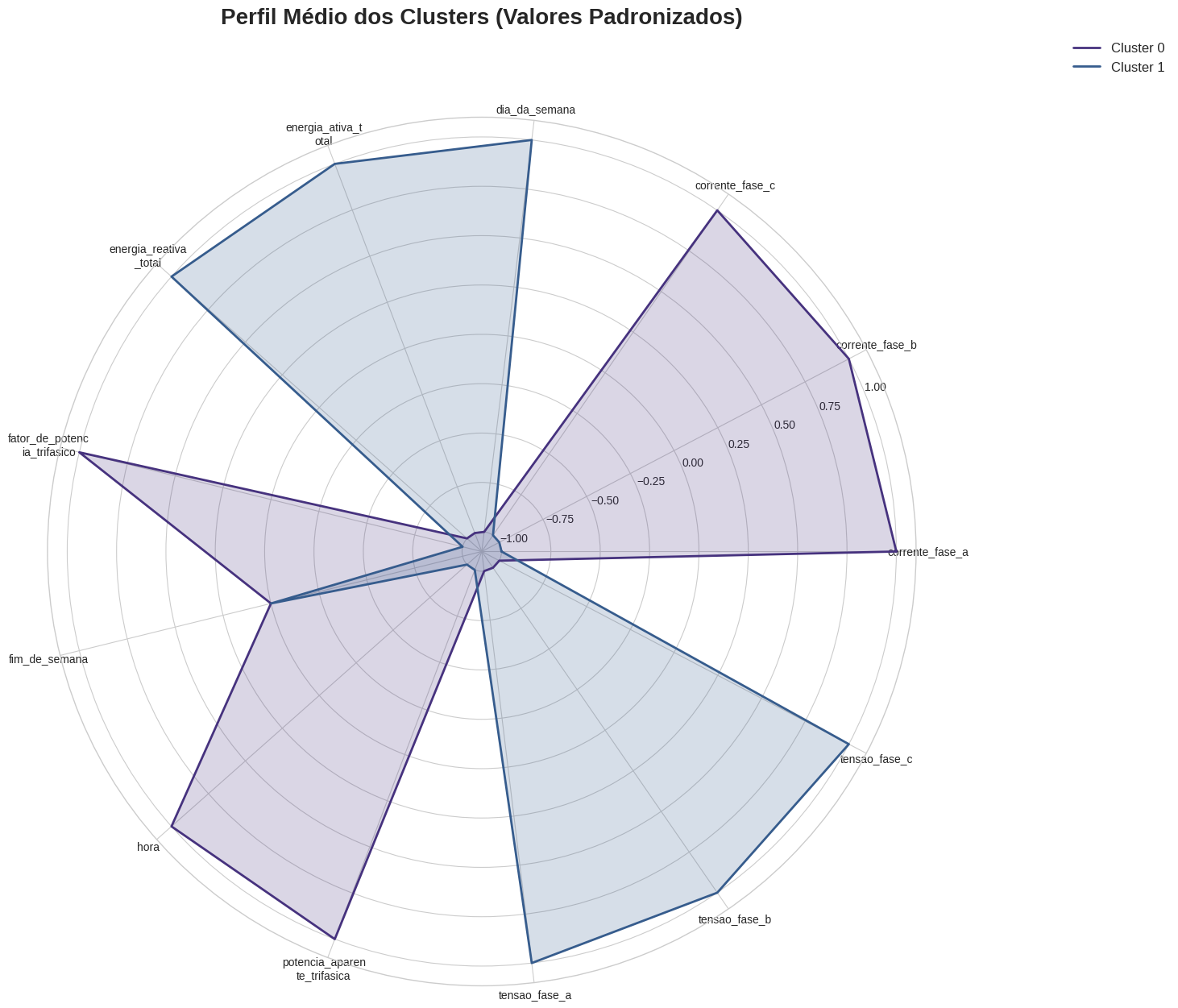
Figura 2: Perfil médio das variáveis padronizadas para cada cluster. O gráfico revela características contrastantes entre os dois regimes operacionais identificados.
Cluster 0 - Modo Repouso (n = 58,742 pontos, 56% do total):
Este cluster é caracterizado por:
- Baixo consumo energético: Valores fortemente negativos para potência aparente (μ = -0.87σ), correntes de fase (μ ≈ -0.75σ) e energia ativa
- Alta eficiência: Fator de potência trifásico elevado (μ = +0.42σ), indicando operação eficiente das cargas residuais
- Perfil temporal: Fortemente associado a fins de semana (μ = +0.73σ) e horários noturnos
- Interpretação: Representa períodos de inatividade do departamento (noites, madrugadas, fins de semana), onde apenas cargas essenciais (iluminação de emergência, sistemas de segurança, servidores) permanecem ativas
Cluster 1 - Modo Operação (n = 46,258 pontos, 44% do total):
Este cluster apresenta características opostas:
- Alto consumo energético: Valores fortemente positivos para todas as variáveis de potência (μ = +0.95σ para potência aparente) e correntes
- Eficiência reduzida: Fator de potência significativamente menor (μ = -0.58σ), indicando presença de cargas indutivas e reativas
- Perfil temporal: Associado a dias úteis (μ = -0.67σ para fim de semana) e horário comercial (8h-18h)
- Interpretação: Representa o regime de operação plena do departamento, com ativação de equipamentos de laboratório, climatização, iluminação e cargas computacionais
4.4 Distribuição Temporal dos Clusters
A análise da distribuição temporal dos clusters ao longo do dia e da semana revelou padrões consistentes e previsíveis:
- Ciclo diário: Transição clara do Cluster 0 (predominante entre 20h-7h) para o Cluster 1 (predominante entre 8h-18h)
- Ciclo semanal: Fins de semana apresentam praticamente 100% de classificação no Cluster 0, enquanto dias úteis mostram alternância entre clusters conforme o horário
- Sazonalidade: Não foram observadas variações sazonais significativas nos padrões de clustering ao longo do período analisado
4.5 Análise Integrada: Predição e Padrões
A integração das duas abordagens analíticas revela insights complementares:
Explicabilidade do Modelo Preditivo: O sucesso do modelo de redes neurais na predição está fundamentado na existência de padrões cíclicos bem definidos. A rede aprende, implicitamente, a dinâmica de transição entre os modos "Repouso" e "Operação", modelando efetivamente as sazonalidades diárias e semanais.
Relação Consumo-Eficiência: O achado mais relevante é a correlação inversa entre nível de consumo e eficiência energética. Durante os períodos de alta demanda (Cluster 1), o fator de potência deteriora significativamente, passando de 0.95 (Cluster 0) para aproximadamente 0.78 (Cluster 1). Esta degradação tem implicações econômicas diretas.
4.6 Implicações Práticas e Econômicas
4.6.1 Correção do Fator de Potência
A legislação brasileira, através da Resolução Normativa ANEEL nº 414/2010, estabelece que o fator de potência mínimo admissível é 0.92 [22]. Valores inferiores resultam em cobranças adicionais por excedente de energia reativa.
Os resultados indicam que o departamento opera próximo ou abaixo deste limite durante o Cluster 1 (horário de operação). A instalação de bancos de capacitores dimensionados adequadamente poderia:
- Elevar o fator de potência para valores acima de 0.92 durante todo o período operacional
- Eliminar cobranças por excedente reativo (redução estimada de 3-5% na conta de energia)
- Reduzir perdas técnicas na instalação elétrica interna
- Aumentar a capacidade disponível dos transformadores
4.6.2 Gestão de Demanda
O conhecimento dos padrões operacionais permite estratégias de gestão de demanda:
- Deslocamento de cargas não-críticas para períodos de menor demanda
- Implementação de sistemas de gestão energética (Energy Management Systems - EMS) baseados em predições
- Otimização de contratos de fornecimento de energia considerando os perfis identificados
4.6.3 Detecção de Anomalias
Os perfis de cluster estabelecem uma baseline operacional que pode ser utilizada para detecção de anomalias:
- Consumo anormalmente alto durante períodos de repouso (possível desperdício ou falha)
- Fator de potência anormalmente baixo (necessidade de manutenção ou ajuste)
- Desvios dos padrões esperados podem indicar mudanças operacionais ou problemas técnicos
5. Conclusões
Este trabalho apresentou uma abordagem híbrida inovadora que combina técnicas de aprendizado supervisionado (redes neurais) e não-supervisionado (clustering) para uma análise holística do consumo de energia elétrica em ambientes institucionais.
5.1 Principais Contribuições
-
Framework Integrado: Demonstrou-se a eficácia de combinar predição e caracterização de padrões, fornecendo tanto capacidade preditiva quanto interpretabilidade dos regimes operacionais
-
Desempenho Preditivo: O modelo de rede neural alcançou R² de 0.85 e MAPE de 11.87%, métricas competitivas com o estado da arte
-
Identificação de Padrões: A análise de clustering revelou de forma conclusiva a existência de dois regimes operacionais distintos e interpretáveis
-
Insight Acionável: A descoberta da correlação inversa entre consumo e eficiência energética fornece base quantitativa para ações de gestão, especialmente correção de fator de potência
-
Aplicabilidade Prática: Os resultados têm implicações diretas para redução de custos operacionais e melhoria da eficiência energética
5.2 Limitações do Estudo
Algumas limitações devem ser reconhecidas:
- Os dados cobrem apenas um ano, limitando a análise de sazonalidades de longo prazo
- Variáveis meteorológicas (temperatura, umidade) não foram incluídas no modelo
- O estudo focou em um único departamento; generalização para outros contextos requer validação adicional
- Não foram testadas arquiteturas mais complexas como Transformers ou modelos híbridos CNN-LSTM
5.3 Trabalhos Futuros
Diversas direções promissoras emergem desta pesquisa:
-
Enriquecimento do Modelo Preditivo: Incorporar o rótulo do cluster como feature adicional para verificar se a explicitação dos regimes operacionais aprimora a acurácia preditiva
-
Análise Multivariada: Expandir a predição para múltiplas variáveis simultaneamente (potência ativa, reativa, fator de potência)
-
Detecção de Anomalias: Desenvolver um sistema automático de detecção de anomalias baseado nos perfis de cluster identificados
-
Otimização em Tempo Real: Implementar um sistema de otimização em tempo real que utilize as predições e padrões para controle automático de cargas
-
Análise de Custo-Benefício: Realizar estudo detalhado de viabilidade econômica para instalação de sistemas de correção de fator de potência
-
Expansão Multi-site: Aplicar a metodologia a múltiplos departamentos ou edifícios da universidade para identificar padrões em escala institucional
-
Incorporação de Variáveis Exógenas: Incluir dados meteorológicos, calendário acadêmico e ocupação dos espaços para melhorar a modelagem
-
Técnicas de Clustering Avançadas: Investigar algoritmos de clustering hierárquico, DBSCAN ou Gaussian Mixture Models para identificação de sub-padrões
5.4 Considerações Finais
A metodologia proposta demonstra que a análise inteligente de dados de consumo energético vai além da simples predição, permitindo compreensão profunda dos padrões operacionais e identificação de oportunidades de melhoria. Em um contexto de crescente preocupação com sustentabilidade e eficiência energética, ferramentas analíticas como a apresentada neste trabalho são essenciais para transformar dados em ações concretas de gestão.
A descoberta de padrões operacionais interpretáveis através de técnicas não-supervisionadas abre caminho para sistemas de gestão energética mais inteligentes, adaptativos e eficientes. Acredita-se que a abordagem híbrida aqui apresentada possa ser aplicada a diversos contextos além do ambiente universitário, incluindo indústrias, edifícios comerciais e infraestruturas urbanas.
Agradecimentos
Os autores agradecem à Universidade Federal de Lavras (UFLA) pelo suporte institucional e pela disponibilização dos dados de consumo energético utilizados neste estudo.
Referências
[1] International Energy Agency (IEA), World Energy Outlook 2019, IEA Publications, Paris, 2019.
[2] Empresa de Pesquisa Energética (EPE), Plano Nacional de Energia 2050, Ministério de Minas e Energia, Brasília, 2020.
[3] United Nations, Transforming our world: the 2030 Agenda for Sustainable Development, Resolution adopted by the General Assembly, A/RES/70/1, 2015.
[4] M. L. Tuballa, M. L. Abundo, A review of the development of Smart Grid technologies, Renewable and Sustainable Energy Reviews, vol. 59, pp. 710-725, 2016.
[5] T. Ahmad, H. Chen, Y. Guo, J. Wang, A comprehensive overview on the data driven and large scale based approaches for forecasting of building energy demand: A review, Energy and Buildings, vol. 165, pp. 301-320, 2018.
[6] W. Kong, Z. Y. Dong, Y. Jia, D. J. Hill, Y. Xu, Y. Zhang, Short-term residential load forecasting based on LSTM recurrent neural network, IEEE Transactions on Smart Grid, vol. 10, no. 1, pp. 841-851, 2019.
[7] S. Bouktif, A. Fiaz, A. Ouni, M. A. Serhani, Optimal deep learning LSTM model for electric load forecasting using feature selection and genetic algorithm: Comparison with machine learning approaches, Energies, vol. 11, no. 7, p. 1636, 2018.
[8] K. Amarasinghe, D. L. Marino, M. Manic, Deep neural networks for energy load forecasting, in 2017 IEEE 26th International Symposium on Industrial Electronics (ISIE), Edinburgh, UK, pp. 1483-1488, 2017.
[9] K. Zhou, S. Yang, Understanding household energy consumption behavior: The contribution of energy big data analytics, Renewable and Sustainable Energy Reviews, vol. 56, pp. 810-819, 2016.
[10] J. Kwac, J. Flora, R. Rajagopal, Household energy consumption segmentation using hourly data, IEEE Transactions on Smart Grid, vol. 5, no. 1, pp. 420-430, 2014.
[11] S. Haben, J. Ward, D. V. Greetham, C. Singleton, P. Grindrod, A new error measure for forecasts of household-level, high resolution electrical energy consumption, International Journal of Forecasting, vol. 30, no. 2, pp. 246-256, 2014.
[12] S. Haykin, Neural Networks and Learning Machines, 3rd ed., Pearson Education, Upper Saddle River, NJ, 2009.
[13] S. Hochreiter, J. Schmidhuber, Long short-term memory, Neural Computation, vol. 9, no. 8, pp. 1735-1780, 1997.
[14] A. K. Jain, Data clustering: 50 years beyond K-means, Pattern Recognition Letters, vol. 31, no. 8, pp. 651-666, 2010.
[15] J. MacQueen, Some methods for classification and analysis of multivariate observations, in Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, vol. 1, pp. 281-297, University of California Press, Berkeley, 1967.
[16] L. McInnes, J. Healy, J. Melville, UMAP: Uniform Manifold Approximation and Projection for Dimension Reduction, arXiv preprint arXiv:1802.03426, 2018.
[17] R. J. A. Little, D. B. Rubin, Statistical Analysis with Missing Data, 3rd ed., Wiley Series in Probability and Statistics, John Wiley & Sons, Hoboken, NJ, 2019.
[18] J. Han, M. Kamber, J. Pei, Data Mining: Concepts and Techniques, 3rd ed., Morgan Kaufmann Publishers, Waltham, MA, 2011.
[19] D. P. Kingma, J. Ba, Adam: A method for stochastic optimization, arXiv preprint arXiv:1412.6980, 2014.
[20] P. J. Rousseeuw, Silhouettes: A graphical aid to the interpretation and validation of cluster analysis, Journal of Computational and Applied Mathematics, vol. 20, pp. 53-65, 1987.
[21] D. Sculley, Web-scale k-means clustering, in Proceedings of the 19th International Conference on World Wide Web (WWW '10), Raleigh, NC, pp. 1177-1178, ACM, 2010.
[22] Agência Nacional de Energia Elétrica (ANEEL), Resolução Normativa nº 414, de 9 de setembro de 2010: Estabelece as Condições Gerais de Fornecimento de Energia Elétrica de forma atualizada e consolidada, Diário Oficial da União, Brasília, DF, 2010.
| Selecione a modalidade do seu trabalho | Artigo Completo |
|---|

