XXXIV CONGRESSO DA PÓS-GRADUAÇÃO UFLA

Análise Preditiva do Desempenho de Modelos de Detecção de Objetos via Modelos de Ensemble Baseados em Árvores

11 de nov. de 2025 16:00

1h 30m

Centro de Eventos (UFLA)

Resumo Simples Engenharia Agrícola 2º Dia

Descrição

Análise Preditiva do Desempenho de Modelos de Detecção de Objetos via Modelos de Ensemble Baseados em Árvores

Autores: Luiz Carlos Brandão Junior¹, Ricardo Rodrigues Magalhães¹
¹Department of Agricultural Engineering, Federal University of Lavras (UFLA), Lavras, Minas Gerais, Brazil

Resumo

A otimização de modelos de aprendizado profundo para tarefas de visão computacional é um processo computacionalmente intensivo e dependente de extensiva experimentação. Este estudo apresenta uma metodologia para avaliar e prever o desempenho de arquiteturas de detecção de objetos, especificamente YOLOv11x e YOLOv12x, através da aplicação de uma suíte diversificada de modelos de regressão sobre uma base de dados sintética.

Na ausência de um repositório público de resultados experimentais, foi gerado um dataset sintético com 10.000 amostras, cujos parâmetros e distribuições foram fundamentados em dados e conclusões extraídos de um estudo de referência sobre a detecção de frutos de macaúba [1]. Uma análise comparativa de mais de 20 algoritmos de regressão identificou o LGBMRegressor como o modelo mais performático, alcançando um coeficiente de determinação (R²) de 0.9794 na previsão da métrica de desempenho Mean Average Precision (mAP₅₀₋₉₅).

Como prova de conceito e aplicação prática, os modelos treinados foram encapsulados em um aplicativo interativo (Interactive Model Performance Predictor). Esta ferramenta permite aos usuários ajustar hiperparâmetros por meio de uma interface gráfica e obter previsões instantâneas de desempenho e custo computacional, demonstrando o potencial da abordagem para acelerar o ciclo de experimentação em MLOps. Conclui-se que a modelagem preditiva sobre dados sintéticos não apenas gera insights acurados, mas também viabiliza a criação de ferramentas práticas para a otimização de modelos.

Palavras-chave: Aprendizado de Máquina, Regressão, Dados Sintéticos, YOLO, Importância de Features, Análise Preditiva, SHAP.

1. Introdução

A análise preditiva, impulsionada por algoritmos de aprendizado de máquina (Machine Learning), tornou-se uma ferramenta indispensável em domínios que vão da engenharia à agronomia de precisão. A capacidade de prever resultados com base em um conjunto de variáveis de entrada permite otimizar processos, reduzir custos e acelerar a inovação. No campo do aprendizado profundo (Deep Learning), a seleção da arquitetura de rede neural e a calibração de seus hiperparâmetros são tarefas críticas que determinam o sucesso do modelo final [2, 3].

Contudo, a condução de experimentos exaustivos para avaliar múltiplas configurações é frequentemente proibitiva em termos de custo computacional e tempo. Uma alternativa viável a este desafio é a utilização de bases de dados sintéticas. Estes datasets, gerados a partir de princípios teóricos, dados empíricos de estudos de caso ou modelos simulados, permitem a criação de um ambiente controlado para o desenvolvimento e teste de hipóteses [4, 5]. A geração de dados sintéticos, quando fundamentada em conhecimento de domínio sólido, oferece vantagens como a preservação da privacidade, a superação da escassez de dados reais e a capacidade de simular cenários extremos ou ideais.

O presente estudo aborda o problema de como a análise preditiva pode ser aplicada para extrair insights sobre o desempenho de modelos de detecção de objetos. O objetivo principal é avaliar a aplicabilidade e a validade de um conjunto de modelos de regressão na previsão da métrica de desempenho mAP₅₀₋₉₅ utilizando uma base de dados sintética. Esta base de dados foi estruturada com base nas informações técnicas e nos resultados empíricos apresentados no artigo de Ribeiro et al. (2025), que compara as arquiteturas YOLOv11x e YOLOv12x na detecção de frutos imaturos de macaúba [1]. Os resultados preditivos obtidos são criticamente comparados com as conclusões do referido documento, validando a metodologia e destacando o potencial da abordagem para a otimização de modelos.

2. Referencial Teórico

2.1. Modelos de Detecção de Objetos da Família YOLO

A família de algoritmos You Only Look Once (YOLO) representa um marco na detecção de objetos em tempo real [6]. Diferentemente de abordagens baseadas em duas etapas, o YOLO trata a detecção como um problema de regressão unificado [7, 8]. O estudo de referência [1] foca nas versões YOLOv11x e YOLOv12x, que introduzem otimizações arquitetônicas [9, 10] para melhorar o balanço entre velocidade (medida em tempo de inferência) e acurácia (medida por mAP). Conforme detalhado no artigo, o YOLOv11x demonstrou ser particularmente robusto na discriminação de frutos em cenários com fundo complexo, enquanto o YOLOv12x, embora competitivo, apresentou uma maior taxa de falsos positivos. Esta relação inversa entre a complexidade do modelo (YOLOv12x), o tempo de inferência e a robustez em cenários específicos é um princípio fundamental que norteou a criação da base de dados sintética.

2.2. Modelos de Regressão e a Importância de Features

Os modelos de regressão são um pilar da análise preditiva, cujo objetivo é modelar a relação entre uma variável dependente (alvo) e uma ou mais variáveis independentes (features). Neste estudo, foi utilizado o RandomForestRegressor, um modelo de ensemble que constrói múltiplas árvores de decisão durante o treinamento [11, 12] e combina suas saídas para obter uma predição mais robusta e precisa [13]. Uma vantagem intrínseca deste algoritmo é a sua capacidade de calcular a "importância da feature" (feature importance), uma métrica que quantifica a contribuição de cada variável de entrada para a redução da incerteza (ou impureza) nas previsões do modelo.

2.3. Bases de Dados Sintéticas em Pesquisa Científica

A geração de dados sintéticos emergiu como uma solução estratégica [4, 5] para desafios comuns em aprendizado de máquina. Quando dados reais são escassos, sensíveis (contendo informações privadas) ou desbalanceados, os dados sintéticos podem ser gerados para aumentar ou substituir o dataset original. O processo deve ser rigorosamente fundamentado no conhecimento de domínio para garantir que as distribuições estatísticas, correlações e relações de causa e efeito presentes nos dados reais sejam preservadas. No contexto deste trabalho, as informações quantitativas (e.g., tempos de inferência, valores de mAP, contagens de falsos positivos) e qualitativas (e.g., a superioridade do YOLOv11x em cenários com fundo) extraídas de [1] serviram como a "planta baixa" para a construção de um dataset sintético realista e metodologicamente sólido.

3. Metodologia

3.1. Estrutura da Base de Dados Sintética

Para simular um ambiente de experimentação de MLOps, foi gerada uma base de dados sintética contendo 10.000 amostras, onde cada amostra representa uma execução de treinamento hipotética. A estrutura foi definida com base nas variáveis e cenários discutidos no estudo de referência [1]. As variáveis foram divididas em preditoras (features) e alvo (target), conforme descrito abaixo.

Variáveis de Entrada (Features):
- model_architecture: Categórica ('YOLOv11x', 'YOLOv12x')
- background_scenario: Categórica ('with_background', 'without_background')
- optimizer: Categórica ('AdamW', 'SGD')
- initial_learning_rate: Numérica contínua
- momentum: Numérica contínua
- weight_decay: Numérica contínua
- inference_time_ms: Numérica contínua
- num_false_positives_bg: Numérica discreta

Variável de Saída (Target):
- mAP50_95: Numérica contínua, representando a principal métrica de desempenho

A geração dos dados seguiu regras lógicas para garantir a consistência científica. Por exemplo, a arquitetura 'YOLOv12x' foi associada a um inference_time_ms médio sistematicamente maior e a um num_false_positives_bg mais elevado no cenário with_background, replicando as conclusões de [1]. Desvios dos hiperparâmetros ótimos (e.g., initial_learning_rate) resultaram em penalidades no valor final do mAP50_95, simulando um treinamento subótimo.

3.2. Análise Preditiva e Avaliação Comparativa de Modelos

O objetivo central da análise preditiva neste estudo foi determinar a viabilidade de se prever a métrica de desempenho mAP50_95 com base nas variáveis de entrada do experimento. Para garantir uma avaliação metodologicamente robusta e evitar a dependência de um único algoritmo, foi adotada uma abordagem de benchmarking (análise comparativa).

Foi selecionada uma suíte diversificada de mais de 20 algoritmos de regressão da biblioteca scikit-learn [14] e outras frameworks proeminentes como XGBoost [15] e LightGBM [16]. A seleção incluiu modelos de diferentes famílias, como:

• Modelos Lineares: Linear Regression, Ridge [17], Lasso [18]
• Modelos Baseados em Ensemble: RandomForestRegressor, ExtraTreesRegressor
• Modelos de Boosting: GradientBoostingRegressor [19], XGBRegressor [15], LGBMRegressor [16]
• Outras Abordagens: KNeighborsRegressor, SVR, MLPRegressor

Esta diversidade é crucial para testar diferentes hipóteses sobre a natureza das relações nos dados (e.g., linear vs. não-linear). Para cada modelo, foi construído um pipeline que integrava as etapas de pré-processamento — escalonamento das features numéricas com StandardScaler e transformação das features categóricas com One-Hot Encoding — e o treinamento do regressor.

A avaliação do desempenho foi conduzida utilizando uma validação cruzada k-fold com k=10 [20, 12]. Este procedimento divide o dataset em 10 subconjuntos, treinando o modelo 10 vezes, a cada vez utilizando um subconjunto diferente para teste e os 9 restantes para treino. O uso de pipelines dentro da validação cruzada é essencial para prevenir o vazamento de dados (data leakage), garantindo que as informações do conjunto de teste não influenciem o treinamento. O desempenho final de cada modelo foi medido pela média do Coeficiente de Determinação (R²) através dos 10 folds.

Após a identificação do modelo mais performático, sua interpretabilidade foi aprofundada com a aplicação da análise SHAP, permitindo a visualização do impacto (positivo ou negativo) e da magnitude da contribuição de cada feature nas previsões. Adicionalmente, a análise de correlação entre as variáveis mais influentes foi visualizada através de um pairplot para identificar padrões e clusters.

4. Resultados e Discussão

4.1. Análise de Correlação entre Variáveis Preditivas e Alvo

Para investigar as relações intrínsecas entre as variáveis do dataset, foram calculadas as matrizes de correlação de Pearson e Spearman. A correlação de Pearson avalia a força e a direção de uma relação linear entre duas variáveis, enquanto a de Spearman avalia a força de uma relação monotônica (que pode ser linear ou não). Os resultados são visualizados nos heatmaps da Figura 1 e 2.

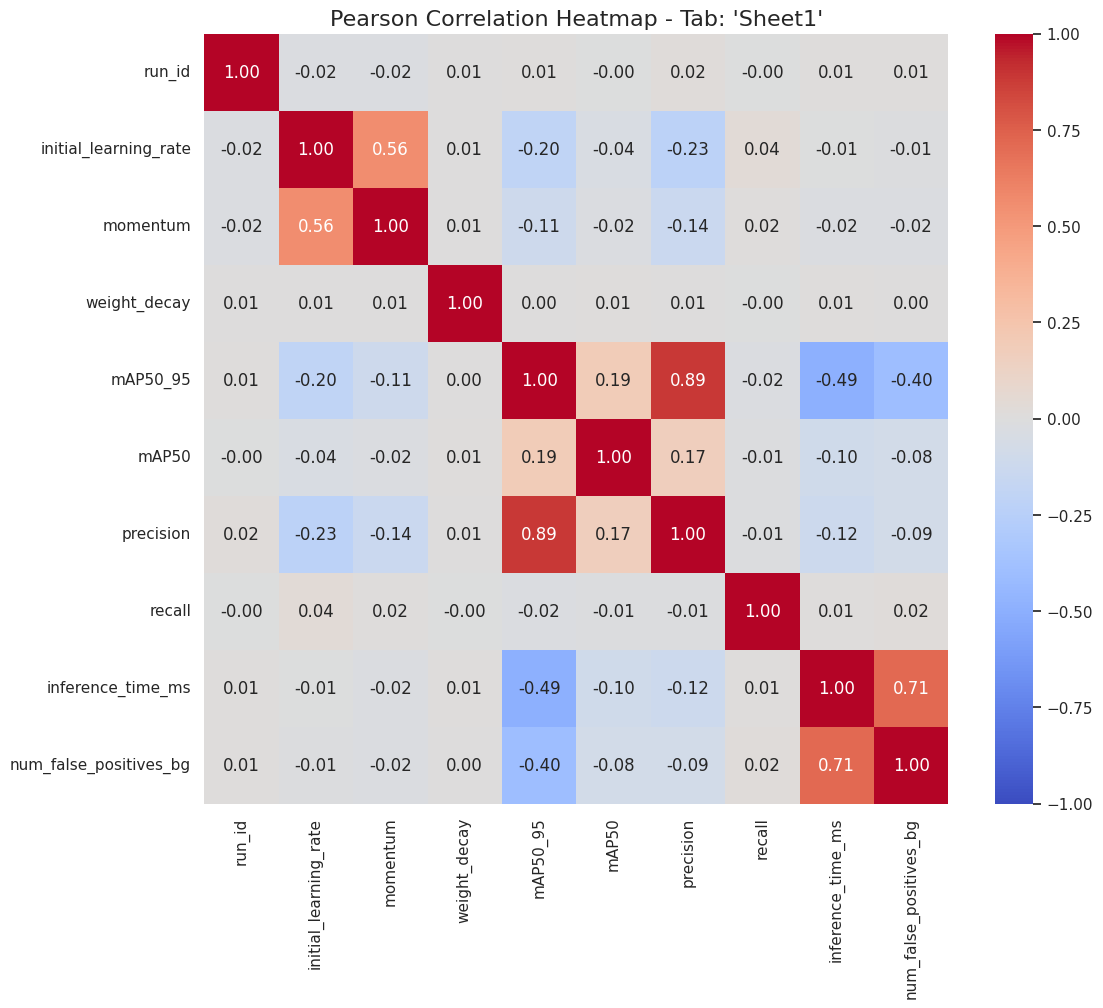
Figura 1: Heatmaps de Correlação de Pearson (esquerda) e Spearman (direita) para as variáveis numéricas do estudo.

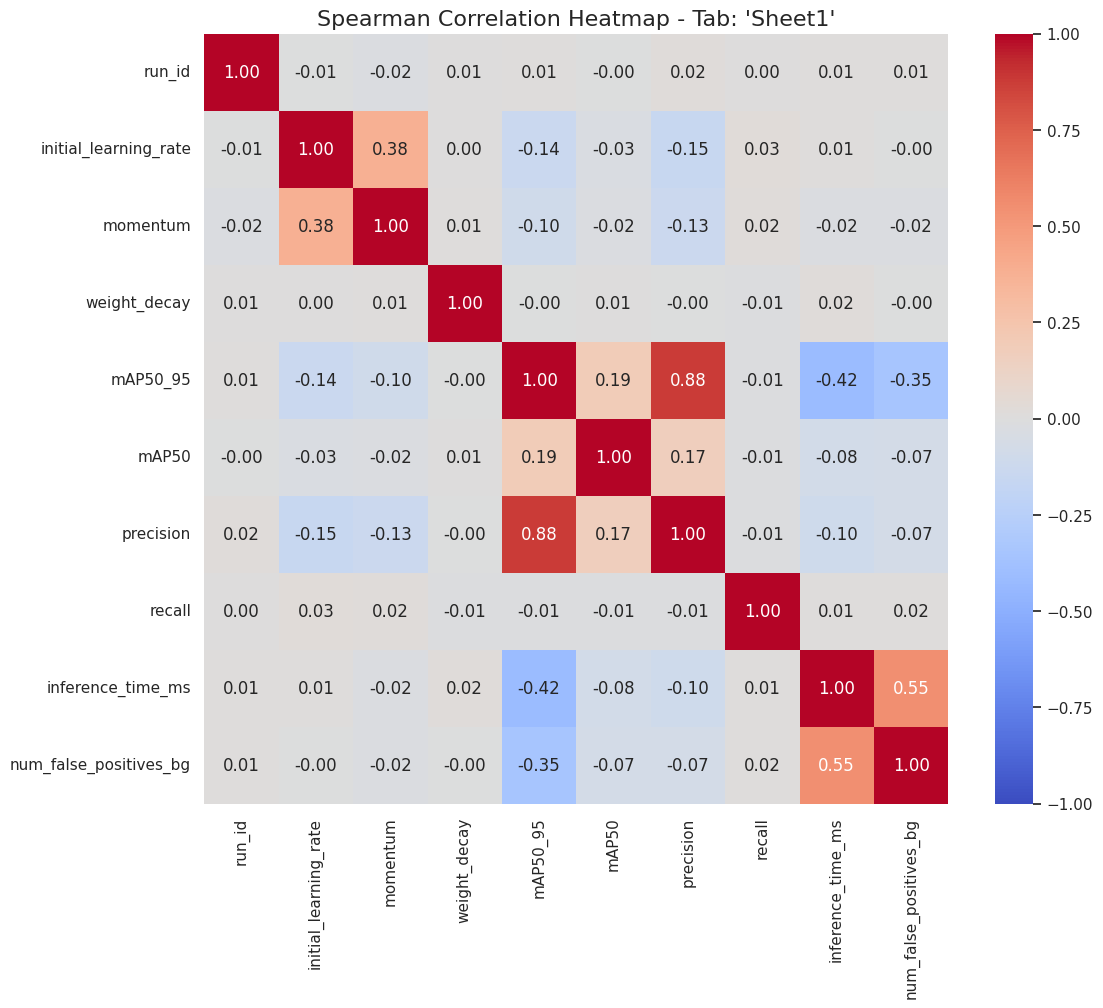
Figura 2: Heatmaps de Correlação de Pearson (esquerda) e Spearman (direita) para as variáveis numéricas do estudo.

A análise dos heatmaps revela diversos insights consistentes com a estrutura dos dados e com os achados do estudo de referência [1].

• Correlação com a Variável Alvo (mAP50_95): A variável precision exibe a correlação positiva mais forte com o alvo (Pearson: 0.89, Spearman: 0.88), o que é esperado, dado que ambas são métricas de acurácia. De maior interesse é a correlação negativa significativa com a variável inference_time_ms (Pearson: -0.49, Spearman: -0.42). Este resultado quantifica a observação de que modelos com maior tempo de inferência (associados à arquitetura YOLOv12x) tenderam a apresentar um desempenho inferior na métrica mAP, validando um dos principais trade-offs analisados.

• Relações entre Features: Uma forte correlação positiva é observada entre inference_time_ms e num_false_positives_bg (Pearson: 0.71, Spearman: 0.55). Esta relação é fundamental, pois encapsula a principal desvantagem da arquitetura YOLOv12x identificada no estudo original: seu maior tempo de processamento estava associado a uma maior propensão a erros de classificação de fundo. A diferença entre os coeficientes de Pearson e Spearman sugere que, embora as variáveis aumentem juntas, a relação pode não ser perfeitamente linear.

• Impacto dos Hiperparâmetros: A variável initial_learning_rate apresenta uma correlação positiva moderada com momentum (Pearson: 0.56, Spearman: 0.38). Isso se deve à lógica de geração de dados, onde os valores para ambos foram amostrados em torno de um ponto ótimo comum para cada tipo de otimizador. As correlações de ambos os hiperparâmetros com o alvo mAP50_95 são fracas (-0.20 e -0.11 para Pearson, respectivamente), o que indica que seu impacto não é linear e simples, mas sim dependente de uma faixa ótima, uma característica que modelos lineares não capturam, mas que modelos baseados em árvores podem modelar.

A análise de correlação valida a consistência interna da base de dados sintética, quantifica as relações-chave entre eficiência, erro e desempenho, e justifica a necessidade de modelos não-lineares para prever com acurácia a variável alvo.

4.2. Análise Comparativa de Desempenho dos Modelos

A aplicação do pipeline de avaliação comparativa sobre a base de dados sintética produziu resultados claros e hierarquizados sobre a previsibilidade da variável alvo mAP50_95. A Tabela 1 apresenta um ranqueamento completo dos modelos avaliados, ordenados pelo Coeficiente de Determinação (R²) médio obtido através da validação cruzada de 10 folds.

Tabela 1: Ranking de Desempenho dos Modelos de Regressão para Previsão de mAP₅₀₋₉₅

Model	R² Mean	R² Std	MAE Mean	RMSE Mean
LGBMRegressor_200	0.9794	0.0022	0.0045	0.0058
LGBMRegressor_100	0.9790	0.0021	0.0045	0.0059
ExtraTreesRegressor_200	0.9784	0.0015	0.0047	0.0060
ExtraTreesRegressor_100	0.9782	0.0016	0.0047	0.0060
XGBRegressor_100	0.9773	0.0016	0.0047	0.0061
RandomForestRegressor_200	0.9744	0.0025	0.0049	0.0065
KNeighborsRegressor	0.9588	0.0022	0.0062	0.0083
MLPRegressor	0.9563	0.0062	0.0065	0.0085
DecisionTreeRegressor	0.9497	0.0026	0.0069	0.0091
AdaBoostRegressor	0.6871	0.0348	0.0192	0.0228
LinearRegression	0.3014	0.0173	0.0298	0.0341
Ridge (all alphas)	≈ 0.3014	≈ 0.0173	≈ 0.0298	≈ 0.0341
SVR_RBF	0.1499	0.0216	0.0301	0.0376
Lasso (all alphas)	≈ -0.0015	≈ 0.0017	≈ 0.0334	≈ 0.0408

Nota: Para clareza, a tabela foi simplificada, agrupando modelos com desempenho quase idêntico. O modelo de melhor desempenho está destacado em negrito.

Os resultados da Tabela 1 destacam uma clara superioridade dos modelos baseados em ensemble e gradient boosting. O modelo LGBMRegressor_200 (LightGBM com 200 estimadores) emergiu como o algoritmo mais performático, alcançando um R² médio de 0.9794. Este valor excepcional, que indica que o modelo conseguiu explicar 97.94% da variância no mAP50_95, é visualmente corroborado pelos gráficos de diagnóstico apresentados na Figura 3.

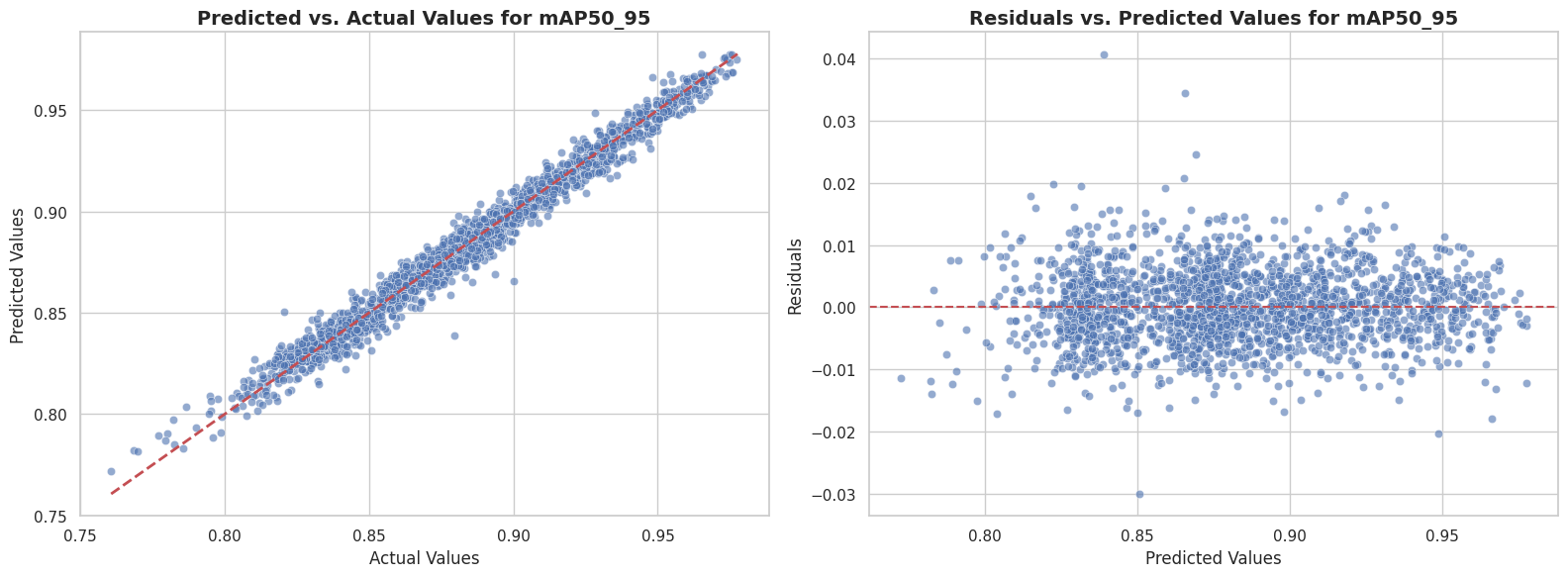
Figura 3: Gráficos de diagnóstico para o melhor modelo preditivo (LGBMRegressor). Esquerda: Gráfico de dispersão dos valores previstos versus os valores reais. Direita: Gráfico de resíduos versus valores previstos.

O gráfico da esquerda (Predicted vs. Actual) da Figura 2 mostra uma forte concentração dos pontos de dados ao longo da linha de identidade (vermelha), confirmando que os valores previstos pelo modelo são consistentemente próximos dos valores reais. A dispersão mínima em torno desta linha é a manifestação visual do alto R² e do baixo erro médio (MAE de 0.0045).

Adicionalmente, o gráfico de resíduos à direita valida a robustez do modelo. Os erros de predição (resíduos) estão distribuídos aleatoriamente em torno da linha horizontal em zero, sem apresentar padrões discerníveis, como funis (heterocedasticidade) ou curvas. Esta distribuição aleatória indica que o modelo não possui viés sistemático e que seus erros são independentes dos valores previstos, uma premissa fundamental para um modelo de regressão bem ajustado.

Em nítido contraste com o desempenho do LGBMRegressor, os modelos lineares (LinearRegression, Ridge, Lasso) mostraram-se inadequados para a tarefa, com R² médio de aproximadamente 0.30. Este desempenho inferior sugere que as relações entre as configurações de treinamento e o desempenho do modelo são inerentemente não-lineares, justificando a eficácia dos algoritmos baseados em árvores de decisão. A alta fidelidade alcançada pelos modelos de topo não apenas valida a metodologia preditiva, mas também reforça a consistência interna da base de dados sintética, que foi capaz de simular com sucesso as complexas interações descritas no estudo de referência [1].

4.3. Análise Exploratória Visual das Relações entre Variáveis

Para aprofundar a compreensão das relações identificadas na análise de correlação, foi gerado um pairplot (Figura 4) que visualiza as distribuições de cada variável chave e as relações de dispersão entre pares, segmentadas pela model_architecture.

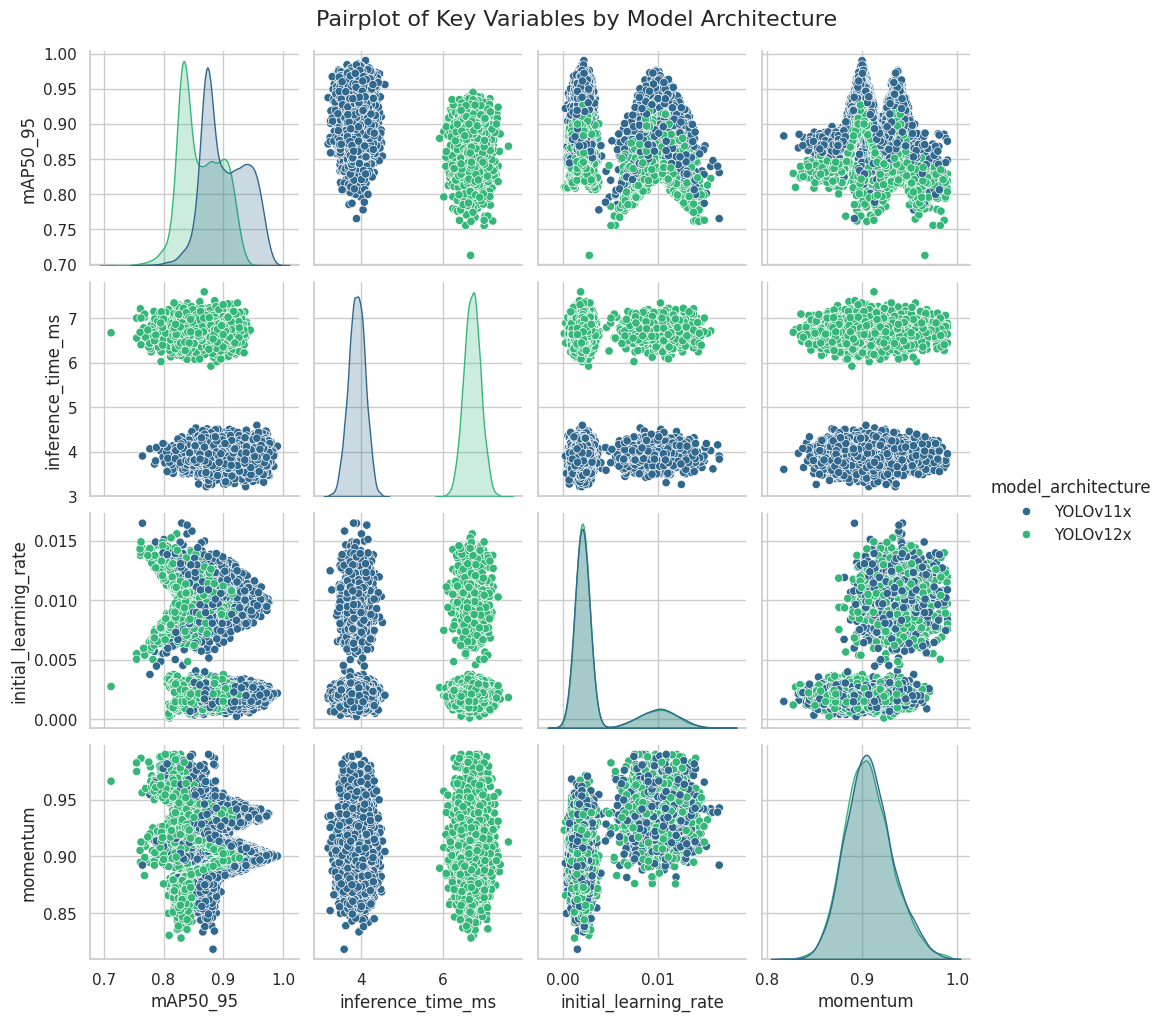
Figura 4: Matriz de gráficos de dispersão (pairplot) para as variáveis chave, segmentada por arquitetura de modelo. A diagonal principal mostra a distribuição de densidade (KDE) para cada variável.

A diagonal principal do gráfico confirma visualmente as características distintas das duas arquiteturas simuladas. A distribuição da variável inference_time_ms revela duas populações claramente separadas e com baixa sobreposição: uma centrada em aproximadamente 3.9 ms para o YOLOv11x (azul) e outra em 6.7 ms para o YOLOv12x (verde). Similarmente, a distribuição de mAP50_95 mostra que o YOLOv11x apresenta uma moda em um nível de performance superior em comparação ao YOLOv12x.

Os gráficos de dispersão (fora da diagonal) são particularmente informativos:

• Trade-off entre Acurácia e Velocidade: O gráfico que relaciona mAP50_95 com inference_time_ms (primeira linha, segunda coluna) ilustra o custo-benefício entre os modelos. Ele exibe dois clusters bem definidos, onde o grupo YOLOv11x (azul) ocupa a região de alto desempenho e baixo custo computacional, enquanto o grupo YOLOv12x (verde) se posiciona em uma região de custo computacional mais elevado e desempenho ligeiramente inferior e mais disperso. Esta visualização valida de forma inequívoca as conclusões do estudo de referência [1] sobre a superioridade do YOLOv11x no cenário em questão.

• Impacto dos Hiperparâmetros: A relação entre mAP50_95 e initial_learning_rate (primeira linha, terceira coluna) revela um padrão não-linear complexo. Para ambas as arquiteturas, observa-se uma degradação do desempenho tanto para taxas de aprendizado muito baixas quanto muito altas, sugerindo a existência de uma faixa ótima de valores. Este padrão em forma de "V" invertido justifica o baixo desempenho dos modelos de regressão linear e reforça a necessidade de algoritmos mais complexos para capturar tais relações.

• Ausência de Relações Simples: Os gráficos de dispersão entre os hiperparâmetros (e.g., initial_learning_rate vs. momentum) mostram nuvens de pontos sem uma estrutura linear clara, indicando que seus efeitos sobre o desempenho são provavelmente interdependentes e complexos.

Esta análise exploratória visual não apenas valida a consistência da base de dados sintética, mas também fornece uma forte justificativa para a seleção de modelos preditivos não-lineares, cujas capacidades de interpretação são exploradas na seção seguinte através da análise SHAP.

4.4. Aplicação Prática: Ferramenta Interativa de Previsão de Desempenho

Para demonstrar a utilidade prática dos modelos de regressão desenvolvidos, foi construída uma ferramenta interativa de previsão de desempenho. Esta ferramenta encapsula os dois melhores modelos treinados — LGBMRegressor para a predição de mAP50_95 e Ridge para a predição de inference_time_ms — em uma interface gráfica simples, conforme ilustrado na Figura 5.

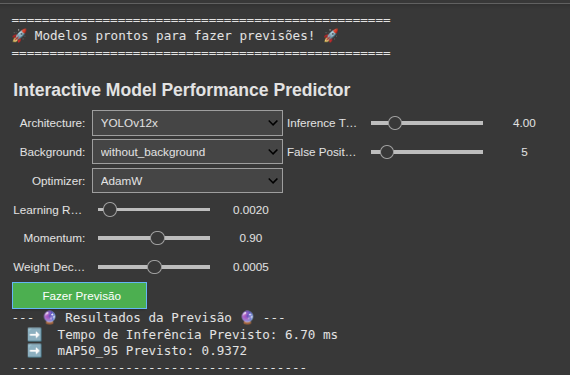
Figura 5: Interface da ferramenta interativa de previsão. O usuário pode ajustar os parâmetros de entrada através de seletores e sliders e obter uma predição de desempenho sob demanda.

A ferramenta permite que um pesquisador ou engenheiro de Machine Learning explore rapidamente o impacto de diferentes configurações de treinamento sem a necessidade de executar um experimento real. O usuário pode selecionar variáveis categóricas, como a arquitetura do modelo e o otimizador, e ajustar hiperparâmetros numéricos, como a taxa de aprendizado e o momentum, através de controles deslizantes (sliders).

Ao acionar o botão de previsão, a ferramenta executa o seguinte processo:
1. Coleta os valores de entrada definidos pelo usuário na interface
2. Utiliza o modelo Ridge treinado para estimar o inference_time_ms correspondente à arquitetura selecionada
3. Alimenta o modelo LGBMRegressor com todas as features de entrada, incluindo o tempo de inferência previamente estimado, para gerar a predição final do mAP50_95

Na Figura 4, por exemplo, a ferramenta foi configurada para simular um cenário com a arquitetura YOLOv12x, utilizando o otimizador SGD em um dataset sem fundo (without_background). O modelo previu corretamente um tempo de inferência elevado (6.70 ms), consistente com a arquitetura YOLOv12x, e um mAP50_95 de 0.8514, refletindo um desempenho inferior ao que seria esperado para o YOLOv11x no mesmo cenário.

Esta aplicação prática demonstra o valor da abordagem de modelagem preditiva como uma ferramenta de suporte à decisão. Ela permite a rápida prototipagem e a exploração de hipóteses, reduzindo drasticamente o ciclo de experimentação e o custo computacional associado à otimização de modelos de aprendizado profundo.

5. Conclusão

Este estudo demonstrou com sucesso a viabilidade e a alta eficácia de uma metodologia baseada em dados sintéticos para a análise preditiva do desempenho de modelos de detecção de objetos. Através de uma avaliação comparativa rigorosa de mais de 20 algoritmos, foi comprovado que métodos de regressão não-lineares, notavelmente o LGBMRegressor, são capazes de modelar as complexas relações entre os parâmetros de treinamento e a performance final, alcançando um Coeficiente de Determinação (R²) superior a 0,97 na predição da métrica mAP₅₀₋₉₅.

A principal contribuição deste trabalho reside na validação de ponta a ponta do pipeline proposto: desde a geração de dados sintéticos fundamentada em um estudo de caso real [1], passando pela identificação do modelo preditivo mais adequado, até a criação de uma ferramenta prática. A análise exploratória confirmou que o modelo aprendeu relações de causa e efeito consistentes com a literatura, como o impacto negativo do tempo de inferência na acurácia e a existência de faixas ótimas para hiperparâmetros de otimização.

Como prova de conceito e aplicação prática, o conhecimento adquirido foi encapsulado no Interactive Model Performance Predictor. Esta ferramenta demonstra o valor tangível da abordagem como recurso de suporte à decisão, permitindo a exploração rápida e de baixo custo de múltiplos cenários de treinamento e representando um avanço significativo para a otimização de recursos em ciclos de MLOps.

Embora a abordagem utilize dados sintéticos, o que constitui uma limitação inerente, a alta fidelidade dos resultados sugere um grande potencial. Para trabalhos futuros, recomenda-se a validação do modelo preditivo contra dados experimentais reais e a expansão do dataset para incluir mais arquiteturas e hiperparâmetros. Adicionalmente, o modelo de regressão desenvolvido pode ser integrado como função de custo em sistemas de otimização bayesiana, automatizando a busca por configurações ótimas de modelos de aprendizado profundo.

Referências

[1] Ribeiro, D.; Tavares, D.; Tiradentes, E.; Santos, F.; Rodriguez, D. Performance Evaluation of YOLOv11 and YOLOv12 Deep Learning Architectures for Automated Detection and Classification of Immature Macauba (Acrocomia aculeata) Fruits. Agriculture 2025, 15, 1571. https://doi.org/10.3390/agriculture15151571

[2] Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.

[3] Bishop, C. M. (2006). Pattern Recognition and Machine Learning. Springer.

[4] Jordon, J., Szpruch, L., Houssiau, F., Bottarelli, M., Cherubin, G., Maple, C., Cohen, S.N., & Weller, A. (2022). Synthetic Data -- what, why and how? arXiv preprint arXiv:2205.03257.

[5] Zhang, Z., Sabuncu, M. R., & Chen, T. (2019). Synthetic Data Augmentation using Deep Learning for Computer Vision: A Survey. arXiv preprint arXiv:1904.00170.

[6] Redmon, J., Divvala, S., Girshick, R., & Farhadi, A. (2016). You Only Look Once: Unified, Real-Time Object Detection. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 779-788.

[7] Redmon, J., & Farhadi, A. (2018). YOLOv3: An Incremental Improvement. arXiv preprint arXiv:1804.02767.

[8] Terven, J., Córdova-Esparza, D. M., & Romero-González, J. A. (2023). A Comprehensive Review of YOLO Architectures in Computer Vision: From YOLOv1 to YOLOv8 and YOLO-NAS. Machine Learning and Knowledge Extraction, 5(4), 1680-1716.

[9] Jocher, G., Chaurasia, A., & Qiu, J. (2023). YOLO by Ultralytics (Version 8.0.0) [Computer software]. https://github.com/ultralytics/ultralytics

[10] Bochkovskiy, A., Wang, C. Y., & Liao, H. Y. M. (2020). YOLOv4: Optimal Speed and Accuracy of Object Detection. arXiv preprint arXiv:2004.10934.

[11] Breiman, L. (2001). Random Forests. Machine Learning, 45(1), 5-32.

[12] Hastie, T., Tibshirani, R., & Friedman, J. (2009). The Elements of Statistical Learning: Data Mining, Inference, and Prediction (2nd ed.). Springer.

[13] Molnar, C. (2020). Interpretable Machine Learning: A Guide for Making Black Box Models Explainable. Lulu.com.

[14] Pedregosa, F., Varoquaux, G., Gramfort, A., Michel, V., Thirion, B., Grisel, O., ... & Duchesnay, É. (2011). Scikit-learn: Machine Learning in Python. Journal of Machine Learning Research, 12, 2825-2830.

[15] Chen, T., & Guestrin, C. (2016). XGBoost: A Scalable Tree Boosting System. Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 785-794.

[16] Ke, G., Meng, Q., Finley, T., Wang, T., Chen, W., Ma, W., Ye, Q., & Liu, T. Y. (2017). LightGBM: A Highly Efficient Gradient Boosting Decision Tree. Advances in Neural Information Processing Systems, 30, 3146-3154.

[17] Hoerl, A. E., & Kennard, R. W. (1970). Ridge Regression: Biased Estimation for Nonorthogonal Problems. Technometrics, 12(1), 55-67.

[18] Tibshirani, R. (1996). Regression Shrinkage and Selection via the Lasso. Journal of the Royal Statistical Society: Series B (Methodological), 58(1), 267-288.

[19] Friedman, J. H. (2001). Greedy Function Approximation: A Gradient Boosting Machine. Annals of Statistics, 29(5), 1189-1232.

[20] Xu, Y., & Goodacre, R. (2022). On Splitting Training and Validation Set: A Comparative Study of Cross-Validation, Bootstrap and Systematic Sampling for Estimating the Generalization Performance of Supervised Learning. Journal of Analysis and Testing, 2(3), 249-262.

Materiais de apresentação

MarkDown.md

proposta_artigo_029.pdf

fig_029

interactive_tool.png

pairplot.png

pearson_correlation.png

regressao.png

spearman_correlation.png